Share this:
Google+
< Previous | Contents | Next >
Simulation of Normally Distributed Random Walk in Microsoft Excel
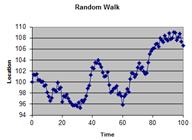
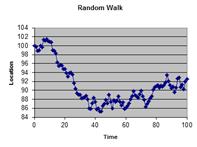
In this section, you will learn how to generate time series data in Microsoft Excel like the following figures. We start with initial location X(0) = 100 and generate the random walk based on normal probability distribution.
First you need to assume the probability distribution. Next, you need to know the initial value. Those are the two inputs of random walk. For our practice, we will create a white noise, that is a random walk based on Gaussian distribution with mean zero and unit variance.
Formula: $$ X_t= X_{t-1} + N(0,1) $$
More general formula of random walk with Gaussian distribution can involve average distribution and standard deviation, thus, the formula becomes
Random walk Formula: $$ X_t= X_{t-1} + \Delta x $$
General Brownian Motion Formula: $$ \Delta x = N(\mu, \sigma) $$
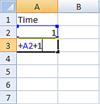
First, we create a column to represent the time. Start with time 1, then in the next cell, add 1 to the cell of previous row.
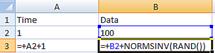
Next, we create a column to represent the time series data based on Brownian motion. We start with 100. Then, we add NORMSINV(RAND()) to the cell of the previous row. NORMSINV is an Microsoft Excel function to generate inverse of Standard Normal distribution (i.e. the value) given the probability. We randomize the probability values. In older version of Microsoft Excel 2003 and below, use NORMINV(RAND(),0,1) to replace NORMSINV(RAND()) because Standard Normal Distribution means the mean is zero and the standard deviation is one.
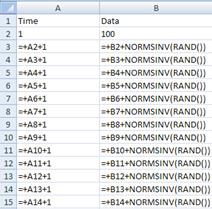
After that you copy the formula of the last row into many rows below.
When you plot the time versus data, you will get the example figure on the left below. Copy the data to the next column and plot the two data will generate the example figure on the right below.
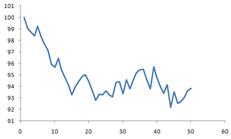
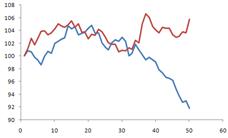
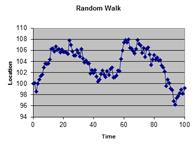
Continue to copy the data to many more rows (up to 500) and plot it will give us example of the figure below. You can press F9 (Function key 9) to recalculate and make new generation of random walk.
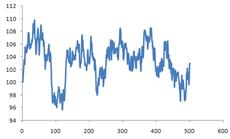
< Previous | Contents | Next >
Do you have question regarding this Stochastic Process tutorial? Ask your question here
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Stochastic Process Tutorial .
http://people.revoledu.com/kardi/tutorial/StochasticProcess/