Matrix Diagonal
A diagonal matrix is a
square matrix
(the same number of rows and columns) whose entries on the diagonal elements are non-zero while all other off-diagonal elements are zero. Diagonal elements are the entries whose index row is equal to column
Example:
If
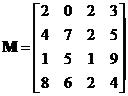then
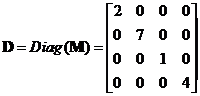
The interactive program below will retain only the diagonal element of the input matrix. The Random Example will generate random square matrix of random order. This program is designed to confirm your basic understanding about diagonal matrix.
Diagonal matrix has several nice properties that the operation on a diagonal matrix is simply equal to the operation on each diagonal element. The operation includes any functions and derivatives but the most well known properties are the following:
-
When two matrices
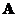and
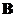are both diagonal matrices, then their matrix multiplication is commutative (which is not true for matrices in general)
-
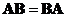
Exponential of a diagonal matrix is equal to exponential of each diagonal element
Example
-
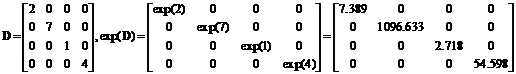
Power of a diagonal matrix is equal to power of each diagonal element
Example
-
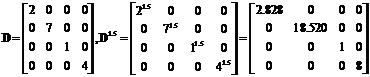
Inverse of a diagonal matrix is equal to reciprocal of each diagonal element
Example
See also : Trace , Is diagonal matrix , diagonalization
Rate this tutorial or give your comments about this tutorial