Matrix Diagonalization
A
square matrix
is
similar
to a square matrix
if there is a non-singular matrix such that
. Let us call matrix
as a
modal
matrix.
Similarity transformation has several properties:
- Identity : a matrix is similar to itself
-
Commutative
: if
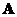is similar to
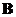then
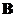is similar to
.
-
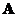Transitive
: if
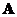is similar to
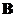and
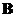is similar to
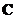, then
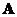is similar to
.
-
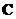If
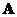is similar to
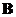then they have
-
Equal
determinant
:
-
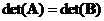
Equal
rank
:
-
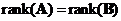
Equal
trace
:
-
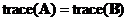
Equal
transpose
:
-
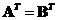
Equal
inverse
:
-
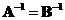
Equal
matrix power
:
-
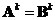
Equal
matrix exponent
:
-
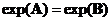
Equal
determinant
:
Since
diagonal matrix
has many nice properties similar to a scalar, we would like to find matrix similarity to a diagonal matrix. The only requirement to perform similarity transformation is to find a
non singular
modal matrix
such that
. We can form modal matrix
from the eigenvector of matrix
. However, we are not sure if the modal matrix
is nonsingular (has inverse).
We know that modal matrix
is nonsingular when the eigenvectors of the square matrix
are being
linearly independent
. But, again we are not sure whether the eigenvectors of the square matrix
will be linearly independent. We only know that if all the eigenvalues of the square matrix
are distinct (do not have any eigenvalue of multiple values) then the eigenvectors are linearly independent. Thus, any square matrix with distinct eigenvalues can be converted into diagonal matrix by similarity transformation
.
To obtain modal matrix
, we perform
horizontal concatenation
of the
linearly independent
eigenvectors
of matrix
such that
. Since eigenvalues of matrix
are all distinct, modal matrix
has full rank because the eigenvectors are linearly independent, therefore modal matrix
has inverse (nonsingular). The diagonal elements of diagonal matrix
consist of the eigenvalues of
.
Example:
Find diagonal matrix of matrix
Solution: First, we find the eigenvector and eigenvalues of matrix
. The matrix has 2 distinct eigenvalues. Eigenvalue
has corresponding eigenvector
and eigenvalue
has corresponding eigenvector
. Since the eigenvalues are all distinct, the matrix is diagonalizable and the eigenvectors are linearly independent.
Next, we form modal matrix
. The inverse modal matrix is
.
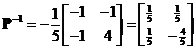Then, we obtain the
diagonal matrix
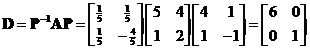. Notice that the diagonal elements are the eigenvalues. Modal matrix
is not
orthogonal matrix
because
.
Example:
Matrix
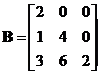has eigenvalues
(with
algebraic multiplicity
of 2) and
(simple). The first eigenvalue
has corresponding eigenvector
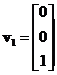and
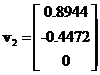. The first eigenvalue
has
geometric multiplicity
of 2 because the two eigenvectors
and
are linearly independent. The second eigenvalue
has corresponding eigenvector
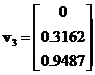. Since matrix
has 3 linearly independent eigenvectors, matrix
is non-defective. We can form modal matrix
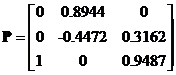such that
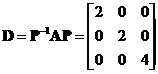. Notice in this example that the eigenvalues are not all distinct but the eigenvectors are linearly independent, therefore the matrix is diagonalizable.
Example:
Matrix
has multiple eigenvalue of
. The eigenvectors associated with eigenvalues are vectors of the form of
for
any non-zero real number. Since the eigenvectors are linearly dependent, the modal matrix
has no inverse and therefore matrix
is non-diagonalizable.
See also : Matrix Eigen Value & Eigen Vector , Matrix Power , Equal matrix
Rate this tutorial or give your comments about this tutorial