Solving Ordinary Differential Equation (ODE)

< Previous | Next | Contents >

Solving ODE using Excel

For this section of introductory tutorial, we will focus first to the first degree and first order ODE. This is because we can always put higher degree ODE into several equations of the first degree ODE.

Solving an ODE means, we have an ordinary differential equation and we want to integrate to get the solution equation

Though theoretically we can solve ODE using integration, in many practical cases, it is very difficult to solve the integration because the existence of the dependent variable in the right hand side of the ODE . We need to go around by solving the integration through an approximation of numerical solution within a range of domain . To solve the ODE numerically, the most widely used solution is using order Runge-Kutta method. Higher order approximation is possible but may be unstable to small variation of initial condition and may lead to a much higher computational cost.

Runge-Kutta (RK) method is a one-step iterative procedure to approximate integration of ODE . Runge-Kutta methods have several advantages compared to many other methods of integration (such as Monte Carlo , Adam-Moulton methods, etc.):

1. No other function is used rather than 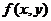is used for the integration,
2. No additional starting values is needed
3. No additional differentiation is needed

The basis of Runge-Kutta methods is Taylor series expansion

We can truncate these expansion terms up to a certain order of error term because for small value of step , higher power of would be very small and negligible.

< Previous | Next | Contents >

See also: Numerical Excel tutorial , Dynamical System tutorial , Kardi Teknomo's Tutorial

Rate this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Solving Ordinary Differential Equation (ODE). https:\\people.revoledu.com\kardi\tutorial\ODE\