Generalized Inverse using Excel
This section of Regression tutorial is very useful to introduce Generalized Inverse matrix. Reading this section may give you a better preparation for further numerical analysis of curvilinear regression, multiple linear regressions and non-linear regression. You may also learn how you can compute linear regression using matrix formula as you may see in the advance statistical books. At least, after reading this section, you may be motivated to begin to read more advance statistical books. They could be very useful for your research or study. Solving the simple linear regression using matrix by itself, however, might not practical because you can use other methods in MS excel to solve linear regression easily.
You may download the spreadsheet example of this tutorial here
Our model is a linear model, say
. If we listed our model for each data, we have
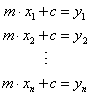
or in matrix form
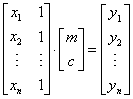
Suppose we name each of them as matrix
, vector
, vector
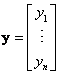and vector
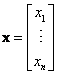, then we can write the equation above in more simple way:
Our objective is to find
given matrix
and vector
. However, matrix
is not a square matrix in general. Thus, we cannot find its inverse. To solve this problem we need a generalized inverse. The trick is to multiply matrix
with its transpose (either form the left or from the right) and the result of this multiplication will become a square matrix that we can find its inverse. We have
Multiplying the two side of the equation with
we get the equivalent
Now we multiply the two side of the equation with
we get the equivalent formula of
Since multiplication of a matrix with its inverse produce identity matrix, we have
Matrix
is called (left) generalized inverse of matrix
.
Note that when we multiply
, we obtain
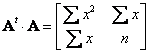
In addition, when we multiply
, we get
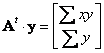
If have read the manual computation you will notice all of those elements are in the formula to compute the slope of regression line.
To do this in Microsoft excel is quite straightforward. We will use the five point data of population as in the manual computation.
1. We type matrix
and vector
from the data and define name
matrix_A
and
vector_y
(using menu
Insert > Name-Define
) for them.
2. Next we get the transpose of matrix
by MS excel function = TRANSPOSE(
matrix_A
) and press Enter. Then highlight the cells where the transpose will be place started from the cell that contains the function. Press F2 and then SHIFT-CTRL-ENTER. You get the transpose matrix and name it
matrix_At
for
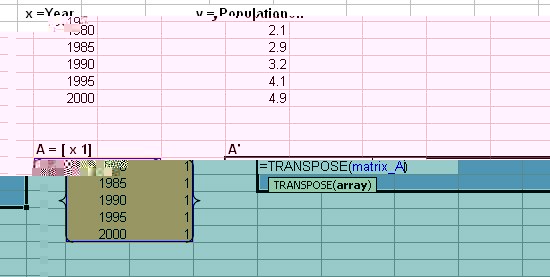
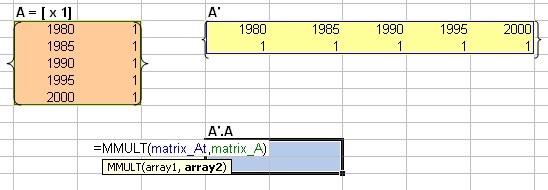
3. We need to obtain
using =MMULT(matrix_At, matrix_A). Hightlight 2 by 2 cells to the right and down from the cell that contain the function. Press F2 and then SHIFT-CTRL-ENTER. Name this
matrix_AtA
.
4. To get the inverse matrix
, we use =MINVERSE(
matrix_AtA
). Hightlight 2 by 2 cells to the right and down from the cell that contain function. Press F2 and then SHIFT-CTRL-ENTER. Name this
inv_At_A.
5. Next, we want to get the generalized inverse matrix
. The size of this matrix should be the same as
. We obtain it by multiplication of the inverse matrix of step 4 with the transpose matrix from step 2. We use MS excel function =MMULT(
inv_At_A
,
matrix_At
). Hightlight 2 by 5 cells to the right and down from the cell that contain the function. Press F2 and then SHIFT-CTRL-ENTER. Name this
matrix_L.
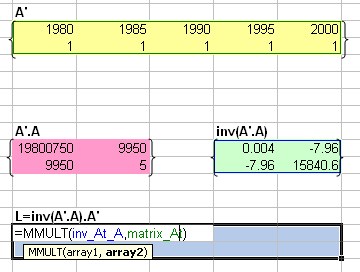
6.
Lastly we multiply the generalized inverse with vector
to find
. Using =MMULT(
matrix_L
,
vector_y
). Hightlight 2 by 5 cells to the right and down from the cell that contain the function. Press F2 and then SHIFT-CTRL-ENTER.
As the result we get
See also: Generalized Inverse
Send your comments, questions and suggestions
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Regression Model using Microsoft Excel. http://people.revoledu.com/kardi/tutorial/Regression/