OLS: Ordinary Least Square Method
For those of you who love mathematics and would like to know from how the linear regression formula was derived, in this section of tutorial you will learn a powerful method called Ordinary Least Square (OLS). I assume that you know calculus to perform the OLS method. Knowing this method is important that you may learn to derive many regression formulas by yourselves.
Let us start with notation.
is data of independent variable from observation
is the mean of
is data of dependent variable from observation
is the mean of
is the estimated of
, that is represented by the regression model.
is the number of observation data
To perform ordinary least square method, you do the following steps:
-
Set a difference between dependent variable and its estimation:
-
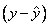
Square the difference:
-
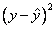
Take summation for all data
-
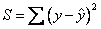
To get the parameters that make the sum of square difference become minimum, take partial derivative for each parameter and equate it with zero,
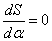
For example:
Find for model parameter for model estimation
using Ordinary Least square!
Answer:
The model only has two parameters, that is
and
.
We take partial derivative of the sum of square difference to the first parameter and equate it to zero
. In taking the partial derivative, we assume
,
and
are constant while
is the only variable.
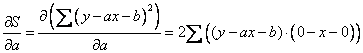
Equate it with zero we have
Actually, the two parameters,
and
, are the real constants and they can go out of the summation sign. Constant 2 is surely not equal to zero, thus we can cancel out to simplify.
We know that
, thus we can simplify the last equation into
(1)
Now, we take partial derivative of the sum of square difference to the second parameter and equate it to zero
. Similar to before, in taking partial derivative, we assume
,
and
are constant, while
is the only variable..
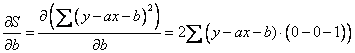
Equate it with zero we have
Actually, the two parameters,
and
, are the real constants and they can go out of the summation sign, Constant 2 is surely not equal to zero, thus we can cancel out to simplify.
We know that
and
,
, thus we can further simplify the last equation into
or,
(2)
Inputting equation (1) into equation (2), we have
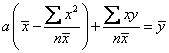
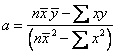
Thus, the parameters of regression model
are
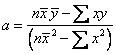and
Notice that the slope
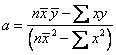is actually equivalent to the
earlier formula of slope
in this tutorial
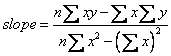by simple algebra.
Example
Find for model parameter for model estimation
using Ordinary Least square!
Answer:
The model only has one parameter
.
We take derivative and equate it to zero
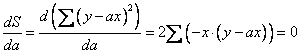
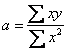
Thus, the parameters of regression model
is
.
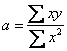You may compare that the slope of the two models
and
are not the same.
Send your comments, questions and suggestions
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Regression Model using Microsoft Excel. http://people.revoledu.com/kardi/tutorial/Regression/