Cayley Distance
Cayley distance measure disorder of ordinal variables by counting the minimum number of transposition of any pair digits on disorder-vectors that at least one digit does not match to the pattern-vector. Unlike Kendall distance that requires adjacent pair, computation of Cayley distance can select any pair digits on the disorder-vector.
The algorithm to compute Cayley distance is to count the minimum number of operation Interchange or transposition of the selected pair:
- Select any pair on disorder-vector that at least one of digit does not match to the corresponding digit in pattern-vector.
- Interchange the order of the pair
Similar to Kendall distance, the problem of Cayley distance computation is to find the
minimum
operation rather than the operation itself. Priority must be given to a pair that its transposition will give higher matched digits between the disorder-vector and the pattern-vector. Unlike Kendall distance, any digit that has already matched does not need to be selected anymore. The matched digits will reduce the number of operation, thus
![]() .
.
Cayley distance is rank invariant that the distance will not change after renumbering of the rank. For example, rank 1 to 10 (best to worst) could be renumbered as rank 10 to 1 (again as the best to worst). While other ordinal distance may change due to this renumbering, Cayley distance and Hamming distance, have nice property that the distance does nit be affected by the rank renumbering.
Example:
We have ask two persons, A and B about their preference on public transport and here is their ordering vector A = [Bus, Van, Train] and B =[Van, Bus, Train]
Suppose we use vector A = [Bus, Van, Train] as pattern-vector and vector B=[Van, Bus, Train] as disorder-vector. Diagram below shows only single interchange operation is needed to transform disorder-vector into pattern-vector. Thus, the Cayley distance of preference between A and B is 1
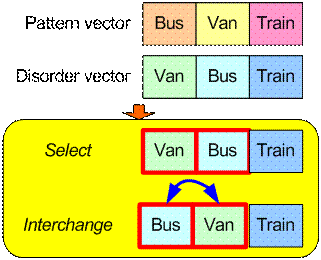
Example:
Suppose we have two judges (A and B) who give rank of importance over 6 products. The ranking vector is given as follow A=[1, 2, 3, 4, 5, 6] and B = [2, 5, 3, 1, 4, 6]. We want to measure Kendall distance between A and B
We set rank vector A as pattern-vector and vector B as disorder-vector. Our goal is to count the minimum number of steps of operation Interchange of any pair to make disorder-vector into pattern-vector. Diagram below show the steps. Since we count three number of interchange, thus the Cayley distance between A and B is 3.
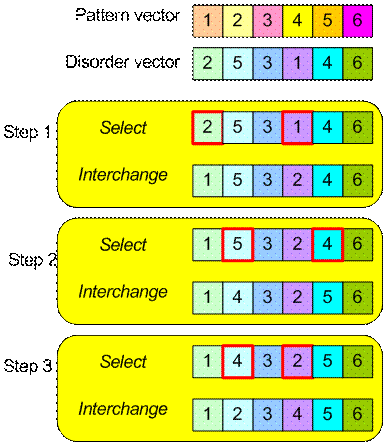
See also: Kendall distance , Hamming Distance for ordinal data
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity

