Hamming Distance

hamming distance

< Previous | Next | Content >

Hamming Distance

Hamming Distance for Binary Variables

Finite binary 0 and 1 sequence is sometimes called a word in coding theory. If two words have the same length, we can count the number of digits in positions where they have different digit. The length of different digits is called Hamming distance. If Hamming Distance Tutorial = number of variables with value 1 for the Hamming Distance Tutorial th objects and 0 for the Hamming Distance Tutorial th object and Hamming Distance Tutorial = number of variables with value 0 for the Hamming Distance Tutorial th objects and 1 for the Hamming Distance Tutorial th object, we have

Formula Hamming Distance Tutorial

Below is an interactive program to compute hamming distance. Try to experiment with your own input values.

Input coordinate values of Object-A and Object-B (the coordinate are binary, 0 or 1), then press "Get Hamming Distance" button. The program will also directly calculate when you type the input.

Features Object A Object B

Example

Feature of Fruit

Sphere shape

Sweet

Sour

Crunchy

Object Hamming Distance Tutorial =Apple

Yes

Yes

Yes

Yes

Object Hamming Distance Tutorial =Banana

No

Yes

No

No

The coordinate of Apple is (1,1,1,1) and coordinate of Banana is (0,1,0,0). Because each object is represented by 4 variables, we say that these objects has 4 dimensions.

Word 1 (Apple)

1

1

1

1

Word 2 (Banana)

0

1

0

0

Is different

Yes

no

Yes

Yes

Since there are 3 digits different ( Hamming Distance Tutorial and Hamming Distance Tutorial ) , we say that the hamming distance is 3.

Other examples:

(1, 1, 1, 0, 0) and

(0, 1, 0, 0, 0) has Hamming distance of 2 because the first and third digit are different.

(1, 0, 0, 1, 1, 0) and

(0, 1, 0, 1, 0, 1) has Hamming distance of 4 because the first, second, fifth and sith digits are different)

(0, 1, 0) and (0, 1, 0) has zero hamming distance because no digit different between the two words.

Hamming distance is somewhat related to Simple matching distance . Hamming distance divided by the length of word (= total number of variables) will give simple matching distance.

Hamming Distance for Ordinal Data

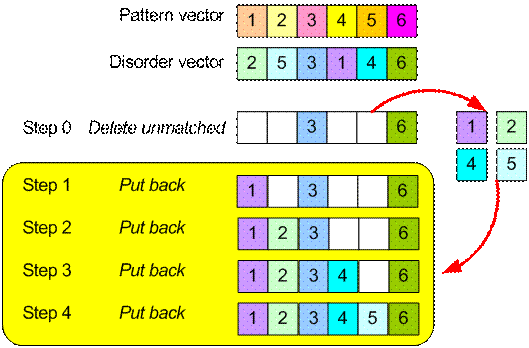
In principle, Hamming distance measure the number of disagreement between two vectors. Hamming distance can also be used for ordinal variables to measure disorder of disorder-vector from a pattern-vector.

The algorithm to compute Hamming distance for ordinal variable involve operation � Putting back � unmatched digit into the correct place, after remove them in the first step:

  1. Take/Delete all unmatched digits on disorder vector that does not match to the corresponding digit in pattern vector
  2. Put the deleted digit one by one into the correct place.

Hamming distance is the count of operation � Putting back �. This algorithm also works for binary variable. Of course, the Hamming distance is equal to the number of unmatched digit.

Example :

Suppose we have two judges (A and B) who give rank of importance over 6 products. The ranking vector is given as follow A=[1, 2, 3, 4, 5, 6] and B = [2, 5, 3, 1, 4, 6]. We want to measure Hamming distance between A and B

We set rank vector A as pattern-vector and vector B as disorder-vector. Our goal is to count the number of steps of operation �Putting back� of digits to make disorder-vector into pattern-vector. Diagram below show the steps. Since we count four number of interchange, thus the Hamming distance between A and B is 4.

Hamming Distance Tutorial

< Content | Previous | Next >

See also: Ordinal Variable , Contents , Ulam Distance

Rate this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity