Jaccard's Coefficient
Jaccard's coefficient (measure similarity) and Jaccard's distance (measure dissimilarity) are measurement of asymmetric information on binary (and non-binary) variables. Compare Jaccard's coefficient with Simple matching coefficient .
For some applications, the existence of
in Simple Matching makes no sense because it represents double absence. This may happen when the value of positive and negative do not have equal information (asymmetry). For example, in matching items the customer purchase in a supermarket using
Market Basket Analysis
, there are more products in the supermarket that the customer does purchase. In this case, the negative value is not important and counting the non-existence in both objects may have no meaningful contribution to the similarity or dissimilarity. Jaccard's coefficient remove the
from simple matching coefficient to become
Formula
Where
= number of variables that positive for both objects
= number of variables that positive for the
th objects and negative for the
th object
= number of variables that negative for the
th objects and positive for the
th object
= number of variables that negative for both objects
= total number of variables
Jaccard's distance can be obtained from
Thus,
To give you more understanding, I provided below an interactive program to compute Jaccard distance and Jaccard Coefficient. Try it yourself your own input values. The examples of computation are given after the program.
Input coordinate values of Object-A and Object-B (the coordinate are binary, number or word), then press "Get Jaccard Cofficient" button to get Jaccard distance and Jaccard Coefficient. The program will directly calculate when you type the input. It will automatically detect whether your inputs are binary or non-binary.
Example
|
Feature of Fruit |
Sphere shape |
Sweet |
Sour |
Crunchy |
Object
=Apple
|
Yes |
Yes |
Yes |
Yes |
|
Object
|
No |
Yes |
No |
No |
=Banana
The coordinate of Apple is (1,1,1,1) and coordinate of Banana is (0,1,0,0). Because each object is represented by 4 variables, we say that these objects has 4 dimensions.
,
and
,
.
Jaccard's coefficient between Apple and Banana is 1/4 . Jaccard's distance between Apple and Banana is 3/4.
For non binary data, Jaccard's coefficient can also be computed using set relations
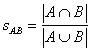
Example 2
Suppose we have two sets
and
.
Then the union is
and the intersection between two sets is
. Jaccard's coefficient can be computed based on the number of elements in the intersection set divided by the number of elements in the union set
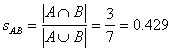
Of course, the set formula is also work for binary data, but we need to compute each digit using Boolean algebra. (A and B is True if both true, A or B is false if both False). Intersection set is equivalent to AND, while Union operation is equivalent to OR.
Example 3
Let us use the example above
|
A |
1 |
1 |
1 |
1 |
|
B |
0 |
1 |
0 |
0 |
|
A and B |
0 |
1 |
0 |
0 |
|
A or B |
1 |
1 |
1 |
1 |
Sum of all digits can be used to compute Jaccard's coefficient
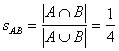the same result as example 1 above.
Note : If your data is binary, you must input as binary in the program above, otherwise it will be detected as non-binary input and you will get incorrect results. For instance, in the Example 1 above, if you input A = (Yes, Yes, Yes, Yes) and B = (No, Yes, No, No), the program will detect as non-binary Jaccard coefficient and produce incorrect Jaccard coefficient of 0.5 (the correct Jaccard coefficient should be 0.25).
This tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity