Kendall Distance

<Content | Previous | Next >

Kendal distance measure disorder of ordinal variables by counting the minimum number of transposition of discordant pair. Discordant pair is adjacent pair digits on disorder-vectors that at least one digit does not match to the pattern-vector.

The algorithm to compute Kendal distance is to count the minimum number of operation “ Interchange ” or transposition of discordant pair:

1. Select adjacent pair on disorder vector that at least one of digit does not match to the corresponding digit in pattern vector (= discordant pair).
2. Interchange the order of the pair

The problem of Kendall distance computation is to find the minimum operation rather than the transposition operation itself.

Example:

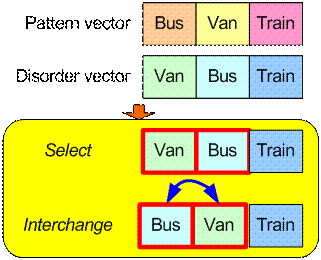
We have ask two persons, A and B about their preference on public transport and here is their ordering vector A = [Bus, Van, Train] and B =[Van, Bus, Train]

Suppose we use vector A = [Bus, Van, Train] as pattern-vector and vector B=[Van, Bus, Train] as disorder-vector. Diagram below shows only single “interchange” operation is needed to transform disorder-vector into pattern-vector. Thus, the Kendal distance of preference between A and B is 1

Example:

Suppose we have two judges (A and B) who give rank of importance over 6 products. The ranking vector is given as follow A=[1, 2, 3, 4, 5, 6] and B = [2, 5, 3, 1, 4, 6]. We want to measure Kendall distance between A and B

We set rank vector A as pattern-vector and vector B as disorder-vector. Our goal is to count the minimum number of steps of operation “ Interchange ” of discordant pair to make disorder-vector into pattern-vector. Diagram below show the steps. Since we count five number of interchange, thus the Kendall distance between A and B is 5.

See also: Cayley distance

<Content | Previous | Next >

Comments for this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Similarity Measurement. http:\\people.revoledu.com\kardi\ tutorial\Similarity\