Footrule Distance
Footrule distance is an absolute distance between two rank vectors. Basically, it is similar to the city block distance or Manhattan distance that used for quantitative variables, but Footrule distance is used for rank.
Other name: Spearman footrule distance
Formula
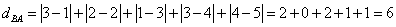
Example:
We have ask two persons, A and B about their preference on public transport and here is their ordering vector A = [Bus, Van, Train] and B =[Van, Bus, Train]
Suppose we set [Bus, Van, Train] as pattern-vector we get rank vector A=[1, 2, 3] and B = [2, 1, 3]. Thus, we can represent the two vectors as two points in three-dimensional space. Point A has coordinate (1, 2, 3) and point B has coordinate (2, 1, 3).
The Footrule distance of preference between A and B is
![]()
Another example (non-unique rank):
You have a pattern vector A = [a, b, c, d, e] that the corresponding rank is a = 1, b = 2, c = 3, d = 4 and e = 5, or in rank vector A = [1, 2, 3, 4, 5]. Then you have another vector B that the corresponding rank is a = 3, b = 2, d = 1, c = 3 and e = 4. Notice that rank of B is non-unique. If you sort the member of set according to the rank it becomes B =[ d, b, a, c, e].
To compute Footrule distance, we need to keep the order of the pattern vector (in this case A = [a, b, c, d, e]), thus rank vector B becomes = [3, 2, 1, 3, 4] .
The footrule distance between A and B is
![]()
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity

