Minkowski Mean

By Kardi Teknomo, PhD.

<Previous | Next | Contents>

Minkowski mean is a generalization of arithmetic, quadratic and harmonic mean.

Minkowski mean is defined as

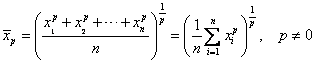
Example:

When , we have Arithmetic mean

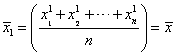
Example:

When , we have Harmonic mean

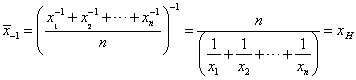
Example:

When p=2, we have Quadratic mean

However, we do not have a specific p in Minkowski mean to represent Geometric mean because Geometric mean is obtained through the limit of parameter p approaches 0, indicated by the formula below

Use the interactive program below to compute Harmonic mean of a list of numbers separated by comma. You may change with your own input values. Try to change the parameter p to a small number but not zero such as 0.0000000001 and compare the result with Geometric Mean.

Table below provides the summary of parameter to relate Minkowski generalized mean and other means.

<Previous | Next | Contents>

See also: Lehmer Mean, Minkowski distance, generalized mean
Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Mean and Average. http:\\people.revoledu.com\kardi\ tutorial\BasicMath\Average\