Harmonic Mean

By Kardi Teknomo, PhD .

< Previous | Next | Contents >

Harmonic Mean

Harmonic mean is the reciprocal of arithmetic mean of reciprocal.

Formula:

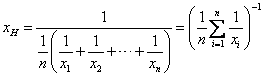
Properties:

• Harmonic mean is always smaller compared to geometric mean , arithmetic mean or quadratic mean .
• To get the correct result, the data values must be all positive

Example:

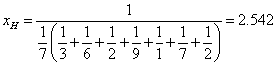
Example applications of Harmonic Means:

• In traffic flow theory , time-mean-speed is an arithmetic mean of speed, while space-mean-speed is a harmonic mean of speed.The speed is measured on the same length of distance travelled.
• In Industrial Engineering, Brown Gibson method uses harmonic means to compute the performance measure of objective factors.
• In Electrical engineering, harmonic means is applied to study the performance of transmission communication systems with relays
  
  

Use the interactive program below to compute Harmonic mean of a list of numbers separated by comma. You may change with your own input values.

< Previous | Next | Contents >

See also: Minskowski mean , Lehmer mean , Generalized Mean
Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Mean and Average. https:\\people.revoledu.com\kardi\ tutorial\BasicMath\Average\