Division of Two Complex Numbers
If we have two complex numbers
and
then we can divide one complex number from another complex number.
Division of two complex numbers is done by rationalization. Rationalization means multiplying both numerator and denominator by the conjugate of the denominator.
Representing in polar form, if
and
then
-
The magnitude is
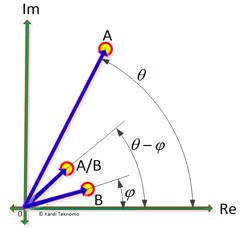
. Division of two complex number produces magnitude of the length ratio of the two factors.
-
The direction is
. Division of two complex number produces difference of angles of the two factors.
Note the argument of the results must be reduced mod
to values in the range of 0 to
.
to values in the range of 0 to
.
.
Graphically, complex division is represented by polar representation illustrated below.
Complex Number Calculator
Properties of Complex Division
-
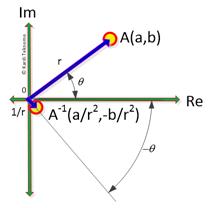
The multiplicative inverse of
is
because
.
is
because
.
because
.
.
- In trigonometric form,
, then
.
, then
.
. - In polar form, If
then
.
then
.
. - Graphically, it is illustrated below.
See Also : Complex Multiplication , Complex Arithmetic , Complex Conjugate
Rate this tutorial or give your comments about this tutorial