Vector Triple Dot Product
Vector triple dot product
is a multiplication of three vectors that produce another vector. First vector
and vector
are multiplied using
inner product
, and then the scalar result of the inner product is used as a
scalar multiple
to the vector
. Geometrically triple dot product is the same as vector scalar multiple that stretch or shrink the vector
based on the angle between vector
and vector
. When the vector
and vector
are collinear the angle is zero and the triple dot product exactly the same as vector
. As the angle between vector
and vector
is larger than zero, the length of vector
reduces up to zero-vector when the angle between vector
and vector
is perpendicular.
Example
Suppose we have three vectors
,
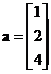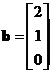and
.
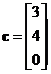First we compute dot product
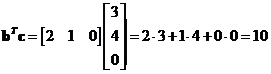
Then, the triple dot product is just scalar multiple of the first vector
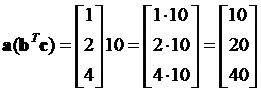
The interactive program below helps you to compute vector triple dot algebraically. You input 3 vectors of the same dimension. The program output is the vector triple dot product. Random example button will generate random vectors at the right format.
Properties
Some important properties of related to triple dot product is
-
Vector triple dot product is related to triple cross product:
-
See Also : Scalar triple product , triple cross product
Rate this tutorial or give your comments about this tutorial