<
Previous
|
Next
|
Contents
>
Non Linear Regression: Power Curve
Assuming that our model is power curve
, we can take logarithm to both sides of the equation.
To compute manually, we take logarithm to both
and
. Thus, we have model transformation
and
.
Example
Data:
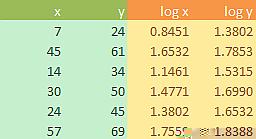
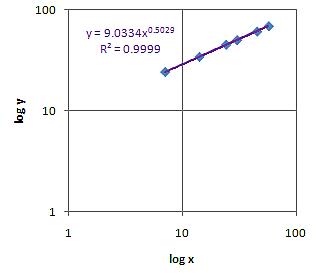
Then we plot log x versus log y and if the data is fit into a power curve, we will obtain a linear model in the double log plot. For our data we find
with R-squared of 0.9999. Thus, the data fits into power curve. The parameters of the power curve can be obtained from the linear model using parameter transformation
and
. In this case, we have
or
. Thus, the regression line is
with the same R-squared of 0.9999
<
Previous
|
Next
|
Contents
>
See Also
:
Regression tutorial
,
Power Rules
,
Logarithm Rules
,
Kernel Regression
Rate this tutorial or give your comments about this tutorial