<
Previous
|
Next
|
Contents
>
Non-Linear Transformation
There are several non-linear curves that that can be transformed into linear curves. Remember that linear curve has straight line relationship. Using non-linear transformation, you can easily solve non-linear problem as a linear (straight-line) problem. In this section, you will learn most commonly used non-linear regression and how to transform them into linear regression.
The following charts show some of the ideas of non-linear transformation.

The following table summarizes the non-linear transformation. The transformation works mostly by taking logarithm. You may want to review
power rules
and
logarithm rules here
.
|
Model |
Model Transformation |
Parameters Transformation |
||
|
Power |
|
|
|
|
|
Exponential-1 |
|
|
|
|
|
Exponential-2 |
|
|
|
|
|
Logarithmic |
|
|
|
|
|
Reciprocal-1 |
|
|
|
|
|
Reciprocal-2 |
|
|
|
|
|
Reciprocal-3 |
|
|
|
|
|
Square Root |
|
|
|
|
Example:
We have the following data
![]()
The scattered and trend curve of the data is shown below. It is clearly non-linear.
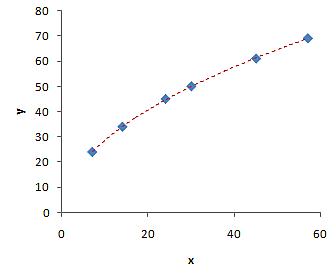
Although we can use MS Excel trend to find the curve directly, for demonstration purposes, we will compute it manually. We will try to compute manually the power curve, logarithmic curve and square root curve.
Click the following links to go directly to the detail and example of each non-linear model:
<
Previous
|
Next
|
Contents
>
See Also : Regression tutorial , Power Rules , Logarithm Rules , Kernel Regression
Rate this tutorial or give your comments about this tutorial
