Canberra Distance

<Previous | Next | Content>

Canberra distance (Lance and Williams, 1967) examines the sum of series of a fraction differences between coordinates of a pair of objects. Each term of fraction difference has value between 0 and 1. The Canberra distance itself is not between zero and one. If one of coordinate is zero, the term become unity regardless the other value, thus the distance will not be affected. Note that if both coordinate are zeros, we need to be defined as . This distance is very sensitive to a small change when both coordinate near to zero.

Formula

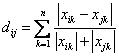
Exercise:
If you have coordinate of object A is (0.001, 0.001) and coordinate of object B is (0.01, 0.01), what is the Canberra Distance? What if due to noise, the coordinate of object A now change to (0.002, 0.001)? Compare it with A = (1000, 1000) and B = (100,100) then change coordinate A into (1002, 1000). How sensitive is the Canberra Distance? Try to experiment with your own input values using the interactive program of Canberra Distance below.

Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Canberra Distance" button. The program will directly calculate when you type the input.

For example:

Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).

The Canberra Distance between point A and B is

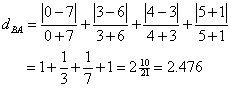
The pattern of Canberra distance in 2-dimension is almost quadrilateral with asymptotic curve in one of the edges. The figure below is drawn with sink at the center. Compare this with the 2D shape of Bray Curtis distance.

See Also: Bray Curtis distance

<Previous | Next | Content>

References:

• Lance G.N., Williams W.T. (1967): Mixed-data classificatory programs, I. Agglomerative Systems. Australian Computer Journal 1:15-20.
• Michel Marie Deza & Elena Deza, Encyclopedia of Distances, Spinger
• Jan Schulz, Canberra Distance, Algorithms - Similarity 

Rate this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Similarity Measurement. http:\\people.revoledu.com\kardi\ tutorial\Similarity\