Minkowski Distance of Order

<Previous | Next | Content>

This is the generalized metric distance. When it becomes city block distance and when , it becomes Euclidean distance. Chebyshev distance is a special case of Minkowski distance with (taking a limit). This distance can be used for both ordinal and quantitative variables.

Formula

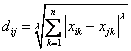
What is the Minkowski distance of the same data when the parameter lambda is -100? What happen if the parameter lambda is zero? What is the Minkowski distance when the parameter lambda is Max? Is the result really the same as Chebyshev distance? What if you change the value of parameter lambda to 50? Try to explore the characteristics of Minkowski distance using your own data and varies the value of parameter lambda. Use the online Minkowski distance program below for your tool of exploration. If you like the program, please recommend this site to your friends.

Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Minkowski Distance" button. The program will directly calculate when you type the input or change the parameter lambda.

For example:

Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).

The Minkowski Distance of order 3 between point A and B is

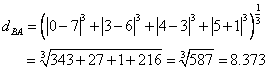
The pattern of Minkowski distance in 2-dimension varies based on the value of parameter Lambda. When the sink is on the center, it forms concentric shapes around the center. When it becomes concentric diamond (City block distance) and when , it becomes concentric circles (Euclidean distance). When Lambda is larger than 2, the shape gradually change from concentric circle to concentric square (Chebyshev distance). Interesting shape below happens when lambda is between 0 and 1.

See also: Minkowski Mean

<Previous | Next | Content>

Rate this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Similarity Measurement. http:\\people.revoledu.com\kardi\ tutorial\Similarity\