Correlation Coefficient
Correlation coefficient is standardized angular separation by centering the coordinates to its mean value. The value is between -1 and +1. It measures similarity rather than distance or dissimilarity.
Other name: linear correlation coefficient, Pearson correlation coefficient
Formula
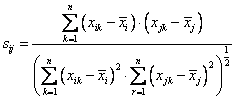, where
and
We define
For example:
|
|
|
Features
|
|
|
|
|
cost |
time |
weight |
incentive |
|
Object A |
0 |
3 |
4 |
5 |
|
Object B |
7 |
6 |
3 |
-1 |
Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).
The mean value of each object is
and
The correlation coefficient between point A and B is
Using MS Excel function CORREL (A, B) gives the same answer as manual computation above.
Exercise
If you have coordinate of object A is (0, 0) and coordinate of object B is (1, 1), what is the correlation coefficient? What happen if you have coordinate of object A is (1000, -1000) while coordinate of object B is (-0.001, 0.001)? What if due to noise, the coordinate of B now change to (-0.002, 0.001)? How sensitive is the correlation coefficient? Compare your result with
Angular Separation
for the same data. Between angular separation and Correlation coefficient, which one do you think is more robust against noise? Try to experiment yourself using the interactive program of Correlation coefficient below.
Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Correlation Coefficient" button. The program will directly calculate when you type the input.
This tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity