Angular Separation
It represents cosine angle between two vectors. It measures similarity rather than distance or dissimilarity. Thus, higher value of Angular separation indicates the two objects are similar. The value of angular separation is [-1, 1] similar to cosine. It is often called as
Coefficient of Correlation
. We need to define
Formula
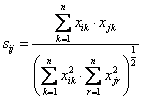
For example :
|
|
|
Features
|
|
|
|
|
|
cost |
time |
weight |
incentive |
|
|
Object A |
0 |
3 |
4 |
5 |
|
|
Object B |
7 |
6 |
3 |
-1 |
Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).
The angular separation between point A and B is
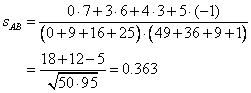
Exercise:
If you have coordinate of object A is (0, 0) and coordinate of object B is (1, 1), what is the angular separation? What happen if you have coordinate of object A is (1000, -1000) while coordinate of object B is (-0.001, 0.001)? What if due to noise, the coordinate of B now change to (-0.002, 0.001)? How sensitive is the Angular Separation? Compare your result with
Correlation coefficient
for the same data. Try to explore your own input using the interactive program of Angular Separation below.
Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Angular Separation" button. The program will directly calculate when you type the input.
How does Angular Separation name come from?
From vector algebra we remember that cosine angle between two vectors can be represented as dot product divided by length of the two vectors
The length of a vector (sometimes called modulus) is the root of square of its coordinate
Putting the two together, we get
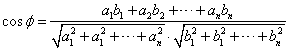
Changing the notation of vectors into coordinate, we get angular separation formula
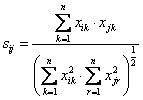
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity