Beginning Data Science: Central Tendency

Average ( mean ), median and mode are the most common measure of central tendency.

Here is an interactive program to calculate Mean, median and mode. Try to explore with your own data. Type a list of numbers separated by comma and click "Get Central Tendency" button. The explanation of each of the central tendency is given below.

Mean

Average or (arithmetic) mean is simply total value of data divided by the number of sample. The formula for mean is

The mean has very nice properties that exactly a half of the data have higher value than the mean and the other half of the data have lower value than the mean. Total deviation of all data toward the arithmetic mean is always zero.

Example, for our data ,

Seconds

Median

Median or middle quartile is computed by sorting your data and then takes the middle value. If you have even number of data, the median is taken by averaging the two middle data as shown in the example below

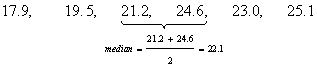
Learning from Data

The general formula for median is

Symbol represents floor function produce the highest integer that smaller than . Symbol denotes ceiling function return the smallest integer that greater than . Notation return the position of our data set after sorted in ascendant way. In our example above, , then , , ,

Mode

Other measurement central tendency of data involves mode that counts the highest number of repetition within your data. Because there is no repetition on your running time data, there is no mode.

Comparison of Mean, Median and Mode

Now, I would like to say that Mode and Mean can sometime misleading. They are not robust measurement for central tendency. Median is robust measurement of central tendency. For example, perhaps because you have run too much, suddenly you feel some pain in your feet, you run again once more but you can only walk instead of running and your "running time" now becomes 79.9 seconds. However, because you have strong spirit and you still insist to record once more, by chance, you measure again your next walking time and you get 79.9 second again. Now you have 8 measurements running time data:

Compare the previous central tendency with the new one:

Central tendency	6 measurements	8 measurements
Mean	21.9 seconds	36.4 seconds
Median	22.1 seconds	23.8 seconds
Mode	Not available	79.9 seconds

If you observe carefully, the first 6 measurements are your running time record, while the last two are walking time and should be excluded from your running time record. If you weren't get sick, the true central tendency of your running time should be around the median value. You see that the last two outlier data does not change the median value so much. The mean value, however, affected very much by the walking time (increase to 36.4 from the true value of 21.9) and the mode is very much affected by random chance.

Thus, median is robust statistic of central tendency against outlier data. Though median is more robust than mean , people still like to use mean because it is easier to compute mean than median . To compute median , we need to sort the data first, and then take the middle value. The sorting is not needed to compute mean .

Median also has a nice property that it minimized the sum of absolute error of the data. The absolute error of our running data above are computed toward mean and median and mode in the following table

Data,
17.9	18.49	5.9	62
19.5	2.38	2.6	60.4
21.2	0.68	0.9	58.7
24.6	1.12	0.9	56.9
23.0	2.72	2.5	55.3
25.1	3.22	3	54.8
79.9	58.02	57.8	0
79.9	58.02	57.8	0
Sum	144.64	131.4	348.1

Mode is very useful when your data is nominal scale . When your data is nominal, you cannot use Mean or Median because it has no meaning. For example, if 1 represent Male and 2 represent Female, the mean or median value of 1.5 has no meaning. Mode gives the highest frequency of the nominal data .

< Previous | Next | Contents >