<
Previous
|
Next
|
Contents
>
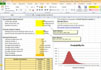M/M/s Queuing Optimization Spreadsheet
is now available only at $9.99
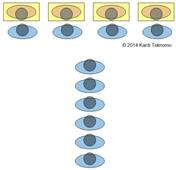
M/M/s Queuing System
When we have a single queue with more than 1 parallel servers, then we have what is called M/M/s queuing system. A diagram below shows 4 parallel servers serving 1 queue. It is important to gain understanding on the difference between M/M/s queuing system with s times M/M/1 queuing system. In M/M/s queuing system we have s parallel servers with 1 queue while s*M/M/1 queuing system we have the same number of servers but we change the configuration to have s number of queues.
The performance for our queuing system where the arrival distribution of customers follows Poisson distribution and the distribution for service time follows Exponential distribution with s number of parallel servers are given by the formulas below.
Use the M/M/s queuing calculator below to experiment and to solve queuing problem of multiple parallel servers. For instance, what happen to the queuing performance if you can increase the number of servers? Which one is better, to increase with one more server or to do training to improve the service rate by 50%? When you set s = 1, you will get exactly the same result as M/M/1 queuing system .
To compute the measurement of effectiveness of the queuing system, first we need to compute the ratio traffic intensity \( \rho = \frac{\lambda}{\mu} \) and the probability that the system is idle \( P_{0} \).
Input:
- Arrival rate (number of customers/unit time) \( \lambda \)
- Service rate (number of customers/unit time) \( \mu \)
- Number of servers \( s \)
Output:
- \( U \) = Utilization factor = percentage of the time that all servers are busy,\( U = \frac{\rho}{s} = \frac{\lambda}{s\mu} < 1 \)
- \( P_{0} \) = probability that there are no customers in the system, \( P_{0} =\left ( \sum_{i=0}^{s-1} \frac{\rho^{i}}{i!} + \frac{\rho^{s}}{s!}\left ( \frac{s\mu}{s\mu-\lambda}\right ) \right )^{-1} \)
- \( P_{n} \) = probability that there are \( n \) customers in the system, \( P_{n}=\begin{cases} \frac{\rho^{n}}{n!} P_{0} & \text{ if } n\leqslant s \\ \frac{\rho^{n}}{s!s^{s-n}} P_{0} & \text{ if } n > s \\ \end{cases} \)
- \( W_{q} \) = average time a customer spends in waiting line waiting for service, \( W_{q}=\frac{L_{q}}{\lambda}\)
- \( W \) = average time a customer spends in the system (in waiting line and being served), \( W=W_{q}+\frac{1}{\mu}=\frac{L}{\lambda} \)
- \( L_{q} \) = average number of customer in waiting line for service, \( L_{q}=\frac{P_{0}\rho^{s+1}}{\left ( s-1 \right )!\left ( s-\rho \right )^{2}} \)
- \( L \) = average number of customer in the system (in waiting line and being served), \( L=\lambda W \)
<
Previous
|
Next
|
Contents
>
Do you have queuing problem? Consult your expert for a solution here
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2014) Queuing Theory Tutorial
http://people.revoledu.com/kardi/tutorial/Queuing/