<
Previous
|
Next
|
Contents
>
Steady State Queuing System
One assumption of queuing theory is to estimate long term behavior of the queuing system. The queuing performance are often called the measurement-of - effectiveness (MOE) in operation research or management science. There are well defined formulas in the queuing theory that are derived from Markov Chain to describe steady state condition operation. The limiting behavior is interesting in the mathematical derivation because it means the system does not change anymore. The system is assumed to be in equilibrium. For each certain number of customers in the system, the rate of transition into the system must be balanced to the rate of transition out of the system. It means the queuing system must be opened 24 hours a day times 7 days a week for infinite number of years. Of course this assumption will never be satisfied in reality.
In reality, this is what happens usually in the queuing system. The system starts with empty and idle condition in the beginning (say, your shops just open in early morning and no customers yet) and then it gradually go into one or more peak time where the number of customers in the system reach the highest level and then gradually reduces. At the end of the service hour (say, in the night before closing of your shop), either the arrival of customers are cut off or there is really no more customers. Thus, the assumption of steady state in the queuing theory does not represent the reality. What does it mean? It means the results of queuing theory is not the same as the results of the observation in the actual queuing system.
For a more general operation of queuing system that can treat both transient and steady state conditions, you may need to use simulation. We can always mimic the actual queuing system through building simulation model. The result of one day service of simulation would be served as one point. If we run the simulation for thousands number of days and plot the average results of the queuing performance over time, we will see a kind of the following figure.
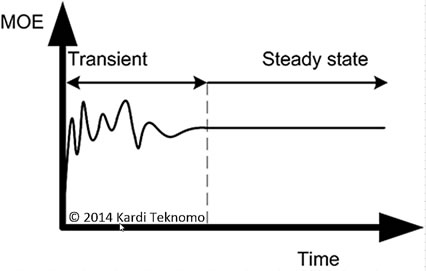
At first, the average results over time will through a kind of transient periods where the queuing performance varies greatly. After a long time, the average queuing performance will reach a stable equilibrium value. Thus, we reach a steady state condition as illustrated in the figure below. Some queuing system may actually never reach the steady state condition because the observation time is not long enough. The results of steady state condition in the simulation would be closed enough to the queuing theory is the two of them use the same assumptions (such as the same arrival distribution, the same service time distribution and queuing discipline, etc.).
<
Previous
|
Next
|
Contents
>
Do you have queuing problem? Consult your expert for a solution here
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2014) Queuing Theory Tutorial
http://people.revoledu.com/kardi/tutorial/Queuing/

